CMake简单使用

西瓜书(《机器学习》作者：周志华)第二章为模型评估与选择，主要是讲解模型评价的指标及其概念。

经验误差

错误率：分类错误的样本数占样本总数的比例。

精度：1-错误率。

误差：学习器的实际预测输出与样本真实输出之间的差异

训练误差：学习器在训练集上的误差。

泛化误差：学习器在新样本上的误差。

过拟合

过拟合：学习器将训练样本本身的一些特点当作了所有潜在样本都会具有的一般性质，也称为过配。过拟合的原因主要是学习器学习能力过于强大。

欠拟合：学习器未将训练样本的一般性质学好，也称为欠配。欠拟合的主要原因是学习器学习能力低下。

评估模型的方法

一般评估模型的指标包括泛化能力、时间开销、存储开销和可解释性等方面。在西瓜书中主要考虑模型的泛化能力这个指标。

测试集：用于测试学习器对新样本的判别能力，近似于泛化误差。（我们的假设：测试样本是从样本的真实分布中独立同分布的——在采样的时候也要保证独立同分布）。

划分测试集和训练集的方法

1. 留出法:将数据集D划分为两个互斥的集合，分别作为训练集、测试集。注意在划分过程中尽量保持数据一致性，通常使用“分层采样”的方式划分。单次划分的结果不准确，一般采用若干次随机划分，重复实验之后取平均值作为评估结果，同时也可以得到估计结果的标准差。
2. 交叉验证法：将数据集划分为k个大小相似的互斥子集，子集通过分层采样的方式产生，然后k-1个子集作为训练集，剩下的1个子集作为测试集，可以产生k组测试集/训练集，进行k次训练测试，最终结果为k组的平均值。交叉验证法的稳定性和保真性受k值影响较大。通常将这种方法称为k折交叉验证。同时，子集存在不同的划分方式，一般需要采取多次k折交叉验证随机划分子集，常见的为”10次10折交叉验证“。当k为样本数量时为交叉验证的特例，留一法（Leave-One-Out，简称LOO）。留一法往往实际被评估的模型与期望评估的用D训练出来的模型接近，但是当数据量较大时，计算的开销可能是无法接受的。
3. 自助法(bootstrapping)：采用自助采样(bootstrapping)为基础，在数据集D基础上，使用自助采样（从数据集中有放回的采样），重复m次，产生m个样本的D’数据集。在数据集中某一样本是可能不被采样的，不被采样的概率为(1-1/m)^m,取极限可得：
   $$
   \lim_\limits{m \to +{\infty}}(1- \frac{1}{m}) = \frac{1}{e} \approx 0.368
   $$
   自助法主要用在数据集较小，难以划分训练/测试集时有用，产生的多个数据集也对集成学习有好处，但是由于自助法改变了初始数据的分布，可能会引入估计偏差。

机器学习参数

机器学习涉及两类参数:算法的参数(也称作超参数,,数量较少)和模型的参数(数量可能较多)。

需要注意,通常将学得模型在实际应用中可能遇到的数据称为测试数据，而训练过程中评估测试模型的数据称为验证集。

模型训练度量

1. 均方误差(mean squared error)：
   $$
   E(f;D)=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^2
   $$
   对于更一般的数据分布$\mit D$和概率密度函数$p(·)$，均方误差可表示为：
   $$
   E(f;\mit D)=\int_{x \sim \mit D}(f(x)-y)^2p(x)dx
   $$

2. 错误率：
   $$
   E(f;D) = \frac{1}{m}\sum_{i=1}^m Ⅱ(f(x_i)\neq y_i)
   $$
   对于一般情况，数据分布$D$和概率密度函数$p(·)$，错误率为：
   $$
   E(f;D)=\int_{x\sim D}Ⅱ(x \neq y)p(x)dx
   $$

3. 精度：
   $$
   acc(f;D)=\frac{1}{m}\sum_{i=1}^m Ⅱ(f(x_i)= y_i)\\
   =1-E(f;D)
   $$
   对于一般情况，数据分布$D$和概率密度函数$p(·)$，精度为：
   $$
   acc(f;D)=\int_{x\sim D}Ⅱ(f(x)=y)p(x)dx\\
   =1-E(f;D)
   $$

查准率、查全率和F1

对于二分类问题，样本根据真实类别和学习器预测类别分为真正例(true positive,TP)、假正例(false positive,FP)、真反例(true negative,TN)和假反例(false negative,FN)。以下为分类结果混淆矩阵：

真实情况	预测结果
	正例	反例
正例	TP	FN
反例	FP	TN

查准率P:
$$
P=\frac{TP}{TP+FP}
$$
查全率R:
$$
R=\frac{TP}{TP+FN}
$$
P-R曲线:查准率-查全率曲线

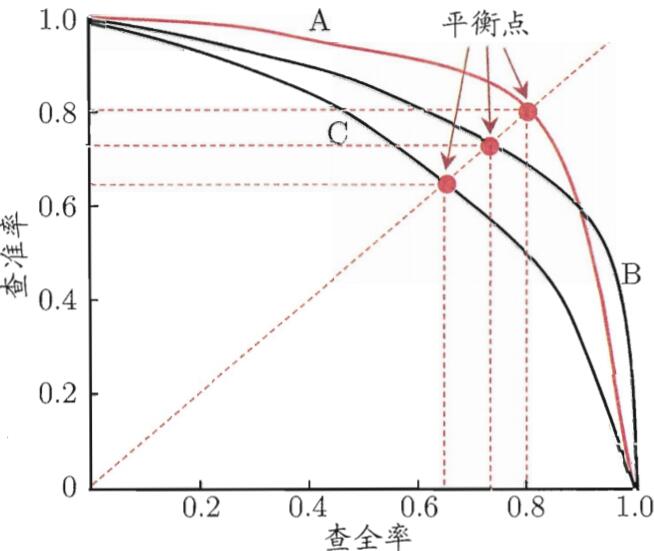
当一条P-R曲线B包住另外一条曲线C时，说明B曲线的模型性能较另外一个C模型好，当如A，B两条曲线时，比较其平衡点(BEP,查准率=查全率)，A的平衡点值较大，说明A的性能较好。除了BEP之外，还常用F1度量：
$$
F1=\frac{2×P×R}{P+R}=\frac{2×TP}{样例总数+TP-TN}
$$
实际上F1是查全率和查准率的调和平均:
$$
\frac{1}{F1}=\frac{1}{2}·(\frac{1}{P}+\frac{1}{R})
$$
F1度量更一般的F_β度量:
$$
F_\beta=\frac{(1+\beta^2)×P×R}{(\beta^2×P)+R}
$$
实际上F_β是查全率和查准率的加权调和平均:
$$
\frac{1}{F_\beta} = \frac{1}{1+β^2}·(\frac{1}{P}+\frac{β^2}{R})
$$
F_β中当β>0时度量查全率对查准率的相对重要性，β=1时为F1。β>1时，查全率有更大影响；β<1时，查准率有更大影响。

当有多个结果混淆矩阵时，可以先计算各自的查准率和查全率，再计算平均值得到”宏查全率”(macro-R)、”宏查准率”(macro-P)以及”宏F1”(macro-F1):
$$
macro\text{-}R = \frac{1}{n}\sum_{i=1}^{n}R_i\\
macro\text{-}P = \frac{1}{n}\sum_{i=1}^{n}P_i\\
macro\text{-}F1 = \frac{2×macro\text{-}P×macro\text{-}R}{macro\text{-}P+macro\text{-}R}
$$

也可以将混淆矩阵先平均再计算平均值，$\overline{TP}$、$\overline{FP}$、$\overline{TN}$、$\overline{FN}$，计算出”微查全率”(micro-R)、”微查准率”(micro-P)以及”微F1”(micro-F1):
$$
micro\text-R=\frac{\overline{TP}}{\overline{TP}+\overline{FN}}\\
micro\text-P=\frac{\overline{TP}}{\overline{TP}+\overline{FP}}\\
micro\text-F1=\frac{2×micro\text{-}P×micro\text{-}R}{micro\text{-}P+micro\text{-}R}
$$

ROC和AUC

ROC(Receiver Operating Characteristic)：“受试者工作特征”曲线。ROC曲线图的纵轴为”真正例率”(True Positive Rate,TPR),横轴为”假正例率”(False Positive Rate,FPR),定义如下:
$$
TPR=\frac{TP}{TP+FN}\\
FPR=\frac{FP}{TN+FP}
$$
当ROC的曲线被包住时，说明后者的性能较好。当交叉时，由AUC(Area Under ROC Curve，ROC曲线下面积)决定。当ROC曲线由点{(x₁,y₁),(x₂,y₂),…,(x_m,y_m)}形成时，AUC为:
$$
AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)·(y_i+y_{i+1})
$$

代价敏感错误与代价曲线

非均等代价（unequal cost）:为权衡不同类型错误所造成的不同损失。
在二分类任务中，可以设定”代价矩阵”(cost matrix)

真实类别	预测类别
	第0类	第1类
第0类	0	cost01
第1类	cost10	0

Ps:一般情况下，重要的是代价的比值而不是绝对值，cost₀₁=100,cost₁₀=50与cost₀₁=2,cost₁₀=1效果是等价的。

“代价敏感”(cost-sensitive)错误率为：
$$
E(f;D;cost)=\frac{1}{m}(\sum_{x_i\in D^+}Ⅱ(f(x_i)\neq y_i)×cost_{01}+\sum_{x_i\in D^-}Ⅱ(f(x_i)\neq y_i)×cost_{10})
$$
在非均等代价之下，ROC不能准确表示总体代价，需要以”代价曲线”(cost curve)衡量总体代价。代价曲线的横轴是取值为[0,1]的正概率代价：
$$
P(+)cost=\frac{p×cost_{01}}{p×cost_{01}+(1-p)×cost_{10}}
$$
其中p是样例为正类的概率；纵轴为取值[0,1]的归一化代价
$$
cost_{norm}=\frac{FNR×p×cost_{01}+FPR×(1-p)×cost_{10}}{p×cost_{01}+(1-p)×cost_{10}}
$$
总体代价为围成的面积，代价曲线如下:

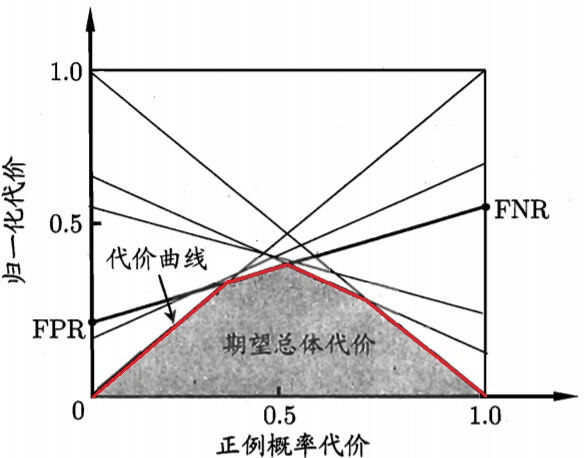
规范化(normalization):将不同变化范围的值映射到相同的固定范围中，常见的为[0,1]，此时称为”归一化”。

比较检验

在现实中，我们使用测试误差$\hat{\epsilon}$假设为模型的泛化误差$\epsilon$。因此，泛化误差为$\epsilon$的模型测得测试误差为$\hat\epsilon$的概率为:
$$
P(\hat\epsilon;\epsilon)={m \choose \hat\epsilon×m}\epsilon^{\hat\epsilon×m}(1-\epsilon)^{m-\hat\epsilon×m}
$$
以下内容为略读

交叉验证t检验：

McNemar检验:

Friedman检验和Nemenyi后续检验:

偏置和方差(略)

参考资料

《机器学习》作者：周志华；

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 qinzhtao@163.com