CMake简单使用

前言

在本章中详细讲解了线性模型，包括线性回归、对数几率回归等等。线性模型形式简单、易于建模，但是蕴含着机器学习中的一些重要的基本思想，并且许多重要的非线性模型也可以在线性模型的基础上引入层级结构或者高维映射得到。此外，线性模型还具有可解释性(comprehensibility,也称为可理解性understandability)。

基本形式：给定示例x=(x₁;x₂;…;x_d)，x_i表示x的第i个属性，线性模型即通过各个属性的线性组合进行预测函数：
$$
f(x)=w_1x_1+w_2x_2+…+w_dx_d+b
$$

向量形式：
$$
f(x)=\boldsymbol{w}^T\boldsymbol{x}+b\\
\boldsymbol{w}=(w_1;w_2;..;w_d)
$$

线性回归

给定数据集$D={(x_1,y_1),(x_2,y_2),…,(x_m,y_m)}$，其中$x_i=(x_{i1};x_{i2};….;x_{id}),y_i\in{\mathbb{R}}$，线性代数试图学得:
$$
f(x_i)=wx_i+b\quad 使得f(x_i)\simeq y_i
$$

求解该模型需要解得$w$和$b$，需要衡量$y_i$和$f(x_i)$之间的差距，一般采用均方误差（又称为平方损失(square loss)）：
$$
(w^*,b^*)=\mathop{\arg\min}\limits_{(w,b)}\sum_{i=1}^{m}(f(x_i)-y_i)^2\\
=\mathop{\arg\min}\limits_{(w,b)}\sum_{i=1}^{m}(y_i-wx_i-b)^2
$$

均方误差具有较好的几何意义，对应常用的欧几里得距离（欧氏距离）。基于均方误差最小化进行模型求解的方法称为最小二乘法（least square method）。求解$w$和$b$使得$E_{(w,b)}=\sum_{i=1}^{m}(y_i-wx_i+b)^2$最小化的过程称为线性回归模型的最小二乘“参数估计”。线性回归模型求解过程如下：

1. 对$E_{(w,b)}$分别对$w$和$b$求偏导
   $$
   \frac{\partial E_{(w,b)}}{\partial w} = 2(w\sum_{i=1}^mx_i^2-\sum_{i=1}^m(y_i-b)x_i),\\
   \frac{\partial E_{(w,b)}}{\partial w} = 2(mb-\sum_{i=1}^m(y_i-wx_i)),
   $$
2. 令偏导值为零可求解出$w$和$b$最优解的闭式解:
   $$
   w = \frac{\sum\limits_{i=1}^my_i(x_i-\overline{x})}{\sum\limits_{i=1}^mx_i^2-\frac{1}{m}(\sum\limits_{i=1}^mx_i)^2}\\
   b = \frac{1}{m}\sum\limits_{i=1}^m(y_i-wx_i),\\
   其中\overline x=\frac{1}{m}\sum\limits_{i=1}^mx_i
   $$

针对更一般的数据集情况，每个样本由$d$个属性组成，则为多元线性回归（又称为多变量线性回归）：
$$
f(\boldsymbol{x}_i)=\boldsymbol{w}^T\boldsymbol{x}_i+b\quad使得f(\boldsymbol{x}_i)\simeq{y}_i
$$
便于表达，将$w$和$b$吸收进向量形式$\hat{w}=(w;b)$，相应的需要将数据集表示为m×(d+1)大小的矩阵$\boldsymbol{X}$
$$
\boldsymbol{X}=\begin{pmatrix}
x_{11} & x_{12} & \ldots & x_{1d} & 1 \\
x_{21} & x_{22} & \ldots & x_{2d} & 1 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
x_{m1} & x_{m2} & \ldots & x_{md} & 1 \\
\end{pmatrix}
$$

同时将标记写为向量形式$\boldsymbol{y}=(y_1;y_2;\ldots;y_m)$则最佳的$w$为：
$$
\hat{w}^*=\arg\min\limits_{\hat w}(\boldsymbol{y}-\boldsymbol{X}\hat{w})^T(\boldsymbol{y}-\boldsymbol{X}\hat{wz})
$$

令$E_{\hat{w}}=(\boldsymbol{y}-\boldsymbol{X}\hat{w})^T(\boldsymbol{y}-\boldsymbol{X}\hat{w})$，对$\hat{w}$求导得:
$$
\frac{\partial E_{\hat{w}}}{\partial\hat{w}}=2\boldsymbol{X}^T{\boldsymbol{X}\hat{w}-y}
$$
当$\boldsymbol{X}^T\boldsymbol{X}$为满秩矩阵或者正定矩阵，令$\hat{w}$偏导值为零可得：
$$
\hat{w}^*=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}
$$

其中$(\boldsymbol{X}^T\boldsymbol{X})^{-1}$为$(\boldsymbol{X}^T\boldsymbol{X})$的逆矩阵。令$\hat{x_i}=(x_i;1)$最终学得多元线性回归模型：
$$
f(\hat{\boldsymbol{x}}_i)=(\boldsymbol X^T\boldsymbol X)^{-1}\boldsymbol X^T\boldsymbol y
$$

然而，$\boldsymbol {X}^T\boldsymbol{X}$往往不是满秩矩阵，例如在许多任务中，样本的变量数目大于样本数，会导致$\boldsymbol{X}$的列数大于行数，$\boldsymbol{X}^T\boldsymbol{X}$显然不是满秩矩阵可以解出多个$\hat{\boldsymbol{w}}$，这时需要对解有所偏好决定，常见的解决方法是引入正则化方法。

线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA）给定训练样例集，设法将样例投影到一条直线上，使得同类的样例的投影点尽可能接近、异类样例的投影点尽可能远离。算法如下图所示：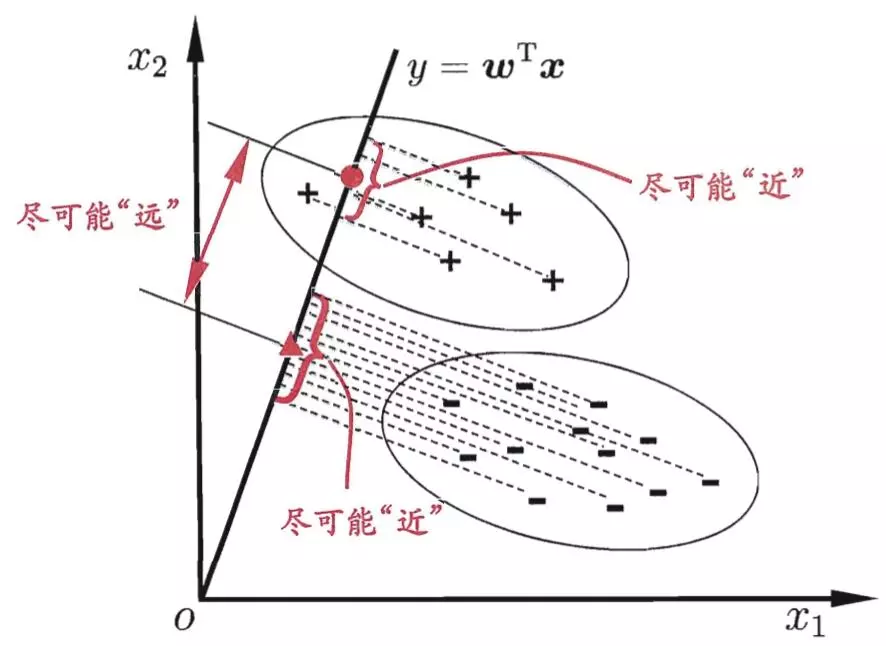

要实现算法，就需要使得类内的协方差尽可能小，类间距离尽可能大。
假设数据集为$D=\{(\boldsymbol{x}_i,y_i)\}^m_{i=1},y_i\in\{0,1\}$,令$\boldsymbol X_i、\boldsymbol{\mu}_i、\boldsymbol{\Sigma}_i$分别表示第$i\in\{0,1\}$类示例的集合、均值向量和协方差矩阵。
类间最大化目标为:
$$
\begin{align}
J &= \frac{\Vert \boldsymbol{\omega^T\mu_0-\omega^T\mu_1} \Vert^2_2}{\boldsymbol{\omega^T\Sigma_0\omega}+\boldsymbol{\omega^T\Sigma_1\omega}}\\
&= \frac{\boldsymbol{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}}{\boldsymbol{\omega^T(\Sigma_0+\Sigma_1)\omega}}
\end{align}
$$

假定类内散度矩阵为：

$$
\begin{align}
\boldsymbol S_\omega &=\boldsymbol{\Sigma_0+\Sigma_1}\\
&=\sum_{\boldsymbol x\in\boldsymbol X_0}\boldsymbol{(x-\mu_0){x-\mu_0}^T+\sum_{\boldsymbol x\in\boldsymbol X_1}\boldsymbol{(x-\mu_1)(x-\mu_1)^T}}
\end{align}
$$
类间散度矩阵为：
$$
\boldsymbol S_b=\boldsymbol{(\mu_0-\mu_1)(\mu_0-\mu_1)^T}
$$
可将$\boldsymbol J$重写为：
$$
\boldsymbol J=\boldsymbol{\frac{\omega^TS_b\omega}{\omega^TS_\omega\omega}}
$$
因为分子分母都有$\boldsymbol\omega$，因此$\boldsymbol J$的解只与$\boldsymbol\omega$的方向有关，与长度无关。可令$\boldsymbol{\frac{\omega^TS_b\omega}{\omega^TS_\omega\omega}}=1$
等价于：
$$
\begin{align}
& \min\limits_{\boldsymbol\omega}\ -\boldsymbol{\omega^TS_b\omega}\\
& \boldsymbol{s.t.}\ \boldsymbol{\omega^TS_\omega\omega}=1
\end{align}
$$
由拉格朗日乘子法，等价于:
$$
\boldsymbol{S_b\omega}=\lambda\boldsymbol{S_\omega\omega}
$$
其中λ拉格朗日乘子，$\boldsymbol{S_b\omega}$方向恒为$\mu_0-\mu_1$，令：
$$
\boldsymbol{S_b\omega}=\lambda(\mu_0-\mu_1)
$$
可得:
$$
\boldsymbol \omega=\boldsymbol{S_\omega^{-1}(\mu_0-\mu_1)}
$$
为了确保解值的稳定性，在实践中对$\boldsymbol{S_\omega}$进行奇异值分解，即$\boldsymbol{S_\omega}=\boldsymbol U\Sigma\boldsymbol V^T$,$\Sigma$为实对角矩阵对角线上的元素为$\boldsymbol S_\omega$的奇异值，再由$\boldsymbol S^{-1}_\omega=\boldsymbol{V\Sigma^{-1}U^{T}}$得到$\boldsymbol S^{-1}_\omega$得到$\boldsymbol S_\omega$。

也可以将LDA扩展到多分类任务中。
全局散度矩阵:
$$
\begin{align}
\boldsymbol S_t&=\boldsymbol S_b+\boldsymbol S_\omega\\
&=\sum^m_{i=1}(\boldsymbol{x_i-\mu})(\boldsymbol{x_i-\mu})^T
\end{align}
$$
其中$\boldsymbol\mu$是所有示例的均值向量，将类内散度矩阵$\boldsymbol S_\omega$重定义为每个类别的散度矩阵之和，即:
$$
\boldsymbol S_\omega=\sum^N_{i=1}\boldsymbol S_{\omega_i}
$$
其中$\boldsymbol S_{\omega_i}$为：
$$
\boldsymbol S_{\omega_i}=\sum_{\boldsymbol x\in X_i}(\boldsymbol x-\boldsymbol\mu_i)(\boldsymbol x-\boldsymbol\mu_i)^T
$$
可得：
$$
\begin{align}
\boldsymbol S_b&=\boldsymbol S_t-\boldsymbol S_\omega\\
&=\sum^N_{i=1}m_i(\boldsymbol\mu_i-\boldsymbol\mu)(\boldsymbol\mu_i-\boldsymbol\mu)^T
\end{align}
$$
多分类LDA可以使用多种实现方法，使用$\boldsymbol S_b,\boldsymbol S_\omega,\boldsymbol S_t$中的两个即可。常见的一种实现是采用优化目标：
$$
\max_{\boldsymbol W}\frac{tr(\boldsymbol W^T\boldsymbol S_b\boldsymbol W)}{tr(\boldsymbol W^T\boldsymbol S_\omega\boldsymbol W)}
$$
其中$\boldsymbol W\in\mathbb R^{dx(N-1)}$,tr(·)表示矩阵的迹，可通过$\boldsymbol S_b\boldsymbol W=\lambda\boldsymbol S_\omega\boldsymbol W$求解。

多分类学习

拆解法：将多分类任务拆分为若干个二分类任务求解。

拆分策略：

1. One Vs. One,将N类两两组合，使用N(N-1)/2个分类器，投票得出结果
2. One Vs. Rest,将N类分为N个1类和（N-1）类分类器分类，根据预测置信进行最终结果判断。
3. Many Vs. Many，正类和反类需要特殊设计，OVO和OVR都是MVM的特殊例子。最常用的是ECOC(Error Correcting Output Codes,纠错输出码)

ECOC算法过程

ECOC过程分为两步：编码和解码。

ECOC编码

对N类进行M次划分，将一部分划为正类，一部分划分为反类，共产生M个数据集，可训练M个二分类器

ECOC解码

M个分类器对样本进行预测，这些预测的标记组成一个编码，将这个编码于各自的编码进行比较，返回其中距离最小的类作为最终的预测结果。

ECOC编码的优点

ECOC具有一定的容错能力。

类别不平衡

概念

类别不平衡（class-imbalance):在分类任务中，不同的类别训练样例数目差别较大的情况。

解决方法

在二分类中常使用$y=\omega^Tx+b$，常使用y>0.5判断为正例，y<0.5判断为反例，因此决策的规则为$\frac{y}{1-y}>1$时为正例。当正反例数不同时，m⁺表示正例数，m^-表示反例数，观测几率为$\frac{m^+}{m^-}$因此可以将判断规则调整为$\frac{y}{1-y}>\frac{m^+}{m^-}$为正例。通过“再缩放”调整类间不平衡，$\frac{y’}{1-y’}=\frac{y}{1-y}×\frac{m^-}{m^+}$。

“再缩放”前提在于无偏采样，但是在实际情概况中是不成立的，因此需采取其他方法：

1. 对反例进行欠采样(undersampling),欠采样若是简单丢弃样本，可能会丢失一些重要的信息。代表算法：Easy-Ensemble:利用集成学习机制，将反例划分成若干不同的集合共学习器使用。
2. 对正例进行过采样（upsampling），欠采样不能简单的重复采样，会导致严重的过拟合，应该采用相应的算法：代表SMOTE，在正例中插值产生额外正例。
3. 使用再缩放的方法，”阈值移动“，同时也是代价敏感学习。

Many Vs. Many 也可以通过DAG(Direct Acyclic Graph)折分法，将分类划分成树状结构，每个节点对应一个分类器。

无偏采样

真实样本中的类别比例在训练集中得以保持。

参考资料

《机器学习》作者：周志华；

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 qinzhtao@163.com